3. Statistiques
Chaque tirage est une épreuve de Bernoulli dont la probabilité de succès (= être à l’intérieur du cercle) est de \(\dfrac{\pi}{4}\) .
Si l’épreuve est répétée n fois, la variable X comptant le nombre de succès suit une loi binomiale d’espérance \(E(X)=n\times\dfrac{\pi}{4}\) et d’écart-type \(\sigma=\sqrt{n\times\dfrac{\pi}{4}\times\left(1-\dfrac{\pi}{4}\right)}\).
Si l’on pose nb_cible le nombre de succès (points à l’intérieur du cercle), n le nombre total de points, l’approximation \(\pi_{mc}\) est le résultat de l’opération \(4\times \dfrac{nb\_cible}{n}\).
Sur un grand nombre de tirages, les valeurs de \(\pi_{mc}\) auront pour moyenne \(\pi\) (puisque E(X) \(\times \dfrac{4}{n} = \pi\) ) et pour écart-type \(\sigma_{mc}=\sigma \times \dfrac{4}{n} = \dfrac{4 \times \sqrt{\dfrac{\pi}{4} \times \left(1-\dfrac{\pi}{4}\right)}}{\sqrt{n}} \approx \dfrac{1,64}{\sqrt{n}}\).
On peut vérifier ce résultat en comparant la valeur théorique de l’écart-type à celle résultant de mesures faites sur des échantillons de tailles variables. Calculons par exemple les valeurs obtenues pour des échantillons de 1 000, 2 000, 3 000… jusqu’à 10 000 points, chacun donnant une valeur de \(\pi_{mc}\). Grâce à une boucle, les mesures seront répétées 10 000 fois pour chaque échantillon.
\(\mu_1\) et \(\sigma_1\) indiquent respectivement la moyenne et l’écart-type obtenus pour chaque groupe de \(\pi_{mc}\).
Quant aux valeurs théoriques, \(\mu_2\) et \(\sigma_2\), elles sont égales à \(\pi\) pour la première et à \(\approx \dfrac{1,64}{\sqrt{n}}\) pour la seconde, selon la formule indiquée ci-dessus.
On peut alors constater que les valeurs effectives obtenues pour ces échantillons sont très proches de celles prévues par la théorie :
import numpy as np
# On utilise le module externe tabulate pour une meilleure présentation
# cf. https://pypi.org/project/tabulate/
from tabulate import tabulate
rng = np.random.default_rng()
loops = 10_000
samples = range(1_000, 11_000, 1_000)
raw_results = []
def get_pi_mc(n):
tab = rng.random((n, 2))
nb_cible = np.sum(tab[:, 0]**2 + tab[:, 1]**2 < 1)
return nb_cible * 4 / n
for n in samples:
tab = np.zeros(loops, dtype=np.float64)
for i in range(loops):
tab[i] = get_pi_mc(n)
mu1, s1 = np.mean(tab), np.std(tab)
s2 = 4 * np.sqrt(np.pi/4 * (1 - np.pi/4)) / np.sqrt(n)
raw_results.append((n, mu1, s1, s2))
# formatage et impression
results = [(n, f'μ1 = {mu1:6f}\nμ2 = {np.pi:6f}',
f'σ1 = {s1:6f}\nσ2 = {s2:6f}')
for n, mu1, s1, s2 in raw_results]
headers=['n\n(échantillon)',
'μ1 (val. effective)\nμ2 (val. théorique)',
'σ1 (val. effective)\nσ2 (val. théorique)']
print(tabulate(results, headers, tablefmt = "grid"))
+-----------------+-----------------------+-----------------------+ | n | μ1 (val. effective) | σ1 (val. effective) | | (échantillon) | μ2 (val. théorique) | σ2 (val. théorique) | +=================+=======================+=======================+ | 1000 | μ1 = 3.141694 | σ1 = 0.051975 | | | μ2 = 3.141593 | σ2 = 0.051930 | +-----------------+-----------------------+-----------------------+ | 2000 | μ1 = 3.141813 | σ1 = 0.036606 | | | μ2 = 3.141593 | σ2 = 0.036720 | +-----------------+-----------------------+-----------------------+ | 3000 | μ1 = 3.141833 | σ1 = 0.029901 | | | μ2 = 3.141593 | σ2 = 0.029982 | +-----------------+-----------------------+-----------------------+ | 4000 | μ1 = 3.141440 | σ1 = 0.025831 | | | μ2 = 3.141593 | σ2 = 0.025965 | +-----------------+-----------------------+-----------------------+ | 5000 | μ1 = 3.141528 | σ1 = 0.023316 | | | μ2 = 3.141593 | σ2 = 0.023224 | +-----------------+-----------------------+-----------------------+ | 6000 | μ1 = 3.141906 | σ1 = 0.021202 | | | μ2 = 3.141593 | σ2 = 0.021200 | +-----------------+-----------------------+-----------------------+ | 7000 | μ1 = 3.141315 | σ1 = 0.019485 | | | μ2 = 3.141593 | σ2 = 0.019628 | +-----------------+-----------------------+-----------------------+ | 8000 | μ1 = 3.141404 | σ1 = 0.018517 | | | μ2 = 3.141593 | σ2 = 0.018360 | +-----------------+-----------------------+-----------------------+ | 9000 | μ1 = 3.141738 | σ1 = 0.017283 | | | μ2 = 3.141593 | σ2 = 0.017310 | +-----------------+-----------------------+-----------------------+ | 10000 | μ1 = 3.141425 | σ1 = 0.016401 | | | μ2 = 3.141593 | σ2 = 0.016422 | +-----------------+-----------------------+-----------------------+
Une autre façon de visualiser la relation entre n et la déviation standard est de représenter cette dernière en fonction de \(\dfrac{1}{\sqrt{n}}\).
On peut utiliser la fonction get_pi_mc() définie ci-dessus pour constituer un nuage de points. On constate alors que la déviation standard exprimée en fonction de l’inverse de la racine carrée du nombre de points total donne un bel alignement (croix rouges sur le graphe ci-dessous).
Et si l’on a installé le module scipy.stats, on peut utiliser la fonction de régression linéaire (lineregress()) qui nous donne les coordonnées de la droite (ligne bleue).
import matplotlib.pyplot as plt
import scipy.stats as sc
# Détermination des valeurs expérimentales
X = np.zeros(len(samples), dtype=np.float64)
Y = np.zeros(len(samples), dtype=np.float64)
for k, n in enumerate(samples):
tab = np.zeros(loops, dtype=np.float64)
for i in range(loops):
tab[i] = get_pi_mc(n)
X[k] = 1/np.sqrt(n)
Y[k] = np.std(tab)
# Représentation d’un nuage de points
plt.plot(X, Y, 'r+')
# Modélisation du graphique
droite = sc.linregress(X, Y)
coefficient = droite.slope
oorigine = droite.intercept
print(f'coefficient directeur : {coefficient:.2f}')
print(f'ordonnée à l’origine : {oorigine:.2f}')
# Tracé de la droite de régression
yline = coefficient * X + oorigine
plt.plot(X, yline, lw=0.5, c='tab:blue')
plt.xlabel(r'$1 \ / \ \sqrt{n}$')
plt.ylabel(r'écart-type ($\sigma$)')
plt.title(r'$\sigma=f \ (1 \ / \ \sqrt{n})$')
plt.show()
coefficient directeur : 1.66 ordonnée à l’origine : -0.00
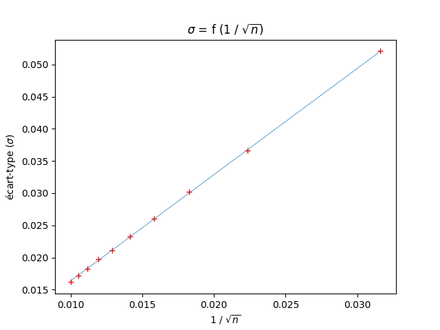
Le coefficient obtenu est proche de celui que prévoit la théorie : \(s=\dfrac{k}{\sqrt{n}}\) avec \(k=4 \times \sqrt{\dfrac{\pi}{4} \times \left(1-\dfrac{\pi}{4}\right)}\) soit environ 1,64.
D’après le théorème central limite, on sait que la loi binomiale suivie par la variable associée au nombre de succès converge en loi vers une loi normale d’espérance \(n\times\dfrac{\pi}{4}\) et d’écart-type \(\sqrt{n\times\dfrac{\pi}{4}\times\left(1-\dfrac{\pi}{4}\right)}\).
Si l’on observe la répartition de 100 000 échantillons de 10 000 points, on voit nettement se dessiner la courbe en cloche de la densité de la loi normale :
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as sc
rng = np.random.default_rng()
def get_nb_success(n):
"""Renvoie le nombre de succès (x² + y² < 1)"""
tab = rng.random((n, 2))
return np.sum(tab[:, 0]**2 + tab[:, 1]**2 < 1)
loops, n = 100_000, 10_000 # 100 000 échantillons de 10 000 pts
data = np.zeros(loops)
for i in range(loops):
data[i] = get_nb_success(n)
loc = n * np.pi / 4 # espérance théorique
scale = np.sqrt(n * (np.pi / 4) * ( 1 - np.pi / 4)) # écart-type théorique
xleft, xright = loc - 4 * scale, loc + 4 * scale
domain = np.linspace(xleft, xright)
plt.hist(data, bins=40, density=True, alpha=.6)
pdf_norm = sc.norm.pdf(domain, loc=loc, scale=scale)
plt.plot(domain, pdf_norm, 'r-', lw=1.6)
plt.xlim(xleft, xright)
plt.xlabel('Nombre de succès')
plt.ylabel('Fréquence normalisée')
plt.title('Loi binomiale et loi normale')
plt.show()
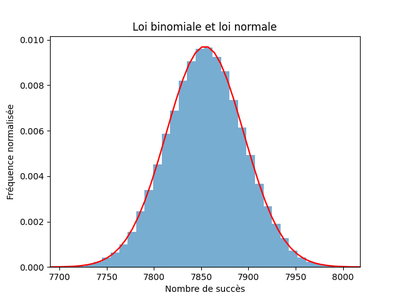
On peut donc utiliser les propriétés des lois normales et calculer les quantiles. Ainsi, au seuil de 95 %, l’intervalle de fluctuation est défini par :
$$ p-1,96 \sqrt{\frac{p \ (1-p)}{n}}\leq\frac{S}{n}\leq\ p+1,96 \sqrt{\frac{p \ (1-p)}{n}}$$
S est la variable aléatoire associée au nombre de succès, p la probabilité qui est égale à \(\dfrac{\pi}{4}\), n le nombre total de points placés.
Par définition, on a \(\pi_{mc}=4\times\dfrac{S}{n}\) et \(4\times p=\pi\).
En multipliant par 4 les termes de cette inégalité, on obtient :
$$\pi-1,96 \ \sigma_{mc}\leq\pi_{mc}\leq\pi+1,96 \ \sigma_{mc}$$ où \(\sigma_{mc}\) est égal à \(4\sqrt{\dfrac{p \ (1-p)}{n}}\) qui est l’écart-type des valeurs de \(\pi_{mc}\).
Pour que \(\pi_{mc}\pm\varepsilon\) englobe \(\pi\) avec un niveau de confiance de 95 %, il faut :
$$ 1,96 \ \sigma_{mc}<\varepsilon \Leftrightarrow n>\dfrac{\left(1,96\times4\sqrt{\dfrac{\pi}{4}\left(1-\dfrac{\pi}{4}\right)}\right)^2}{\varepsilon^2}$$
Pour changer le seuil, il suffira de remplacer le coefficient 1,96 par un autre quantile de la fonction de répartition de la loi normale centrée réduite.
En utilisant cette formule, on peut définir une fonction qui calcule le rang de n qu’il faut atteindre pour obtenir \(\pi\) avec une précision et un niveau de confiance donnés. De même, il est possible de calculer la précision atteinte pour un nombre n de points et pour un intervalle de confiance connus.
Enfin, si le nombre de points et la précision sont connus, cette fonction nous renvoie la probabilité que les valeurs de \(\pi_{mc}\) calculées atteignent ce niveau de précision pour cette valeur de n.
Voici à quoi peut ressembler une telle fonction :
from statistics import NormalDist
import locale
import numpy as np
locale.setlocale(locale.LC_ALL, '')
X = NormalDist(0, 1) # loi normale centrée réduite
rng = np.random.default_rng() # initialisation PRNG
def oracle(n=None, prec=None, prob=0.5):
k = X.inv_cdf(prob + (1 - prob) / 2) # fonction quantile
v = 4 * np.sqrt(np.pi / 4 * (1 - np.pi / 4)) # ~ 1,64
if prec and not n:
n = int(( k * v / prec )**2) + 1
elif n and not prec:
prec = round(k * v / np.sqrt(n), 6)
elif n:
k = prec * np.sqrt(n) / v
prob = round(X.cdf(k) - X.cdf(-k), 6)
return n, prec, prob
Voici quelques exemples de ce qu’on peut demander à oracle() :
- Donner le nombre de points qu’il faut placer pour avoir 50 % de résultats proches de \(\pi\) à 0,001 près.
n, *_ = oracle(prec=1e-3)
print(f'{n:n} points sont nécessaires.')
1 226 858 points sont nécessaires.
- Pour avoir \(\pi\) avec une précision de 0,01 dans une proportion de 95 %.
n, *_ = oracle(prec=0.01, prob=95/100)
print(f'{n:n} points sont nécessaires.')
103 596 points sont nécessaires.
- Quelle est la précision obtenue par 45 % des \(\pi_{mc}\) sur un total de 1 million de points ?
_, prec, _ = oracle(n=1e6, prob=45/100) # # 3
print(f'45 % seront compris dans l’intervalle [π - {prec:.3f}; π + {prec:.3f}].')
45 % seront seront compris dans l’intervalle [π - 0.001; π + 0.001].
- Quelle proportion de \(\pi_{mc}\) auront une précision d’au moins 0,0001 sur 2 millions de points ?
*_, prob = oracle(n=2_000_000, prec=0.0001)
print(f'{prob * 100:.2f} % des résultats seront proches de π à moins de 0.0001 près.')
6.86 % des résultats seront proches de π à moins de 0.0001 près.
Ces résultats peuvent être vérifiés expérimentalement en examinant la proportion de \(\pi_{mc}\) répondant aux conditions demandées (nombre et précision) dans des échantillons aléatoires.
import numpy as np
rng = np.random.default_rng()
def verif(n, prec):
"""
Renvoie la proportion de pi_mc obtenues pour n et pour une précision
donnée, l’expérience étant répétée pour 100 échantillons.
"""
loops = 100 # on prend 100 échantillons
nb_cible = np.zeros(loops)
for i in range(loops):
tab = rng.random((n, 2))
nb_cible[i] = np.sum(tab[:, 0]**2 + tab[:, 1]**2 < 1)
return nb_cible[abs(4 * nb_cible/n - np.pi) < prec].size
for n, prec in [(1_226_858, 0.001),
(103_596, 0.01),
(1_000_000, 0.001),
(2000_000, 0.0001)]:
print(verif(n, prec), end=' ')
51 97 49 7
Le tableau ci-dessous permet de comparer les proportions théoriques calculées auparavant et celles obtenues expérimentalement par la fonction verif().
| nombre de points précision | proportion théorique (%) | proportion échantillons (%) |
|---|---|---|
| 1 226 858 0,001 | 50 | 51 |
| 103 596 0,01 | 95 | 97 |
| 1 000 000 0,001 | 45 | 49 |
| 2 000 000 0,0001 | 7 | 7 |
Comme le générateur de nombres pseudo-aléatoires n’a pas été initialisé ici avec un seed, les résultats peuvent être légèrement différents d’un appel de la fonction à l’autre.
Néanmoins, on remarque que les résultats expérimentaux restent assez proches de la valeur théorique, ce qui confirme que la loi normale est ici une bonne approximation.
La relation entre les valeurs de \(\pi_{mc}\) et l’écart-type qui est fonction de \(\dfrac{1}{\sqrt{n}}\) montre que pour obtenir un chiffre de précision supplémentaire, il faut multiplier le nombre de points par 100.
La loi normale permet d’approcher la loi binomiale \(\mathit{B}\left(n, \dfrac{\pi}{4}\right)\) et renseigne sur les intervalles de confiance encadrant les résultats obtenus.
Cependant, si l’on cherche des résultats particuliers grâce à la méthode de Monte-Carlo, les lois statistiques qui décrivent des tendances générales ne sont pas les outils les mieux adaptés.
Si l’on s’intéresse à des résultats précis, il faut revenir à la distribution discrète qui est à la base de cette approximation. Chaque point ajouté modifie \(\pi_{mc}\) qui est — rappelons-le — le résultat d’une division de deux entiers : \(\dfrac{4\times nb\_cible}{n}\).
Ce qui retient ici notre attention, c’est que ces approximations sont obtenues à partir de fractions. Et parmi ces fractions, on sait qu’il en est de remarquables.
Les plus connues sont sans doute 22 / 7 (qui donne \(\pi\) avec 2 décimales exactes) et 355 / 113 (6 décimales exactes), ces deux valeurs approchées de \(\pi\) ayant été proposées dès le Ve siècle de notre ère par le mathématicien chinois Zu Chongzhi (祖冲之).